

基本内容

注明：在”倍角公式“前，皆为高考考纲内容。

任意角三角函数 & 弧度制

略。

图象与性质

注：图象中的竖直线，其实是“五点法”作图的思想，即分别令 sin/cos/tan 里面的数等于$0,\dfrac\pi2,\pi,\dfrac32\pi,2\pi$。

正弦

设正弦函数$f:y=\sin(x)$。

图像

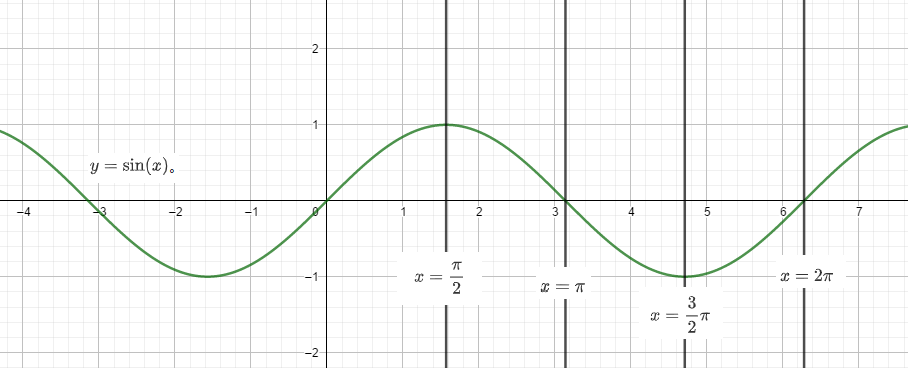
性质

• $\text{dom}f=\mathbb{R},\text{ran}f=[-1,1]$
• 对称性：f关于$(k\pi,0)$中心对称，关于$x=k\pi+\dfrac\pi2$轴对称（$k\in\mathbb{Z}$）。
• 奇偶性：奇函数。
• 周期性：最小正周期为$2\pi$
• 连续性：在$\mathbb{R}$上连续。
• 可导性：在$\mathbb{R}$上可导。
• 单调性：在区间$[2k\pi-\dfrac\pi2,2k\pi+\dfrac\pi2]$上单增，在区间$[2k\pi+\dfrac\pi2,2k\pi+\dfrac32\pi]$单减（$k\in\mathbb{Z}$）。
• 凹凸性：在区间$[(2k+1)\pi,(2k+2)\pi]$上为凹函数，在区间$[2k\pi,(2k+1)\pi]$上为凸函数。
• 有界性：在$\mathbb{R}$上有上界1，有下界-1。

余弦

设余弦函数$f:y=\cos(x)$。

图像

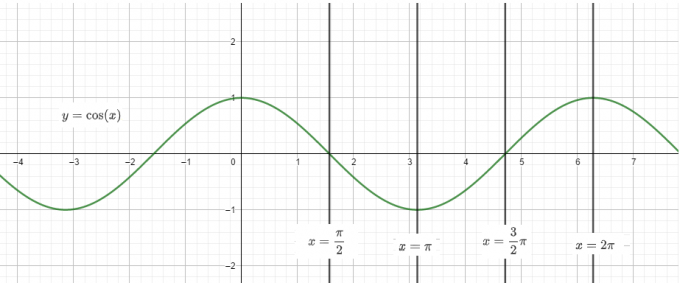
性质

• $\text{dom}f=\mathbb{R},\text{ran}f=[-1,1]$
• 对称性：f关于$(2\pi+k\pi,0)$中心对称，关于$x=k\pi$轴对称（$k\in\mathbb{Z}$）。
• 奇偶性：偶函数。
• 周期性：最小正周期为$2\pi$
• 连续性：在$\mathbb{R}$上连续。
• 可导性：在$\mathbb{R}$上可导。
• 单调性：在区间$[2k\pi-\pi,2k\pi]$上单增，在区间$[2k\pi,2k\pi+\pi]$单减（$k\in\mathbb{Z}$）。
• 凹凸性：在区间$[2k\pi+\dfrac\pi2,2k\pi+\dfrac32\pi]$上为凹函数，在区间$[2k\pi-\dfrac\pi2,2k\pi+\dfrac\pi2]$上为凸函数。
• 有界性：在$\mathbb{R}$上有上界1，有下界-1。

正切

设正切函数$f:y=\tan(x)$。

图象

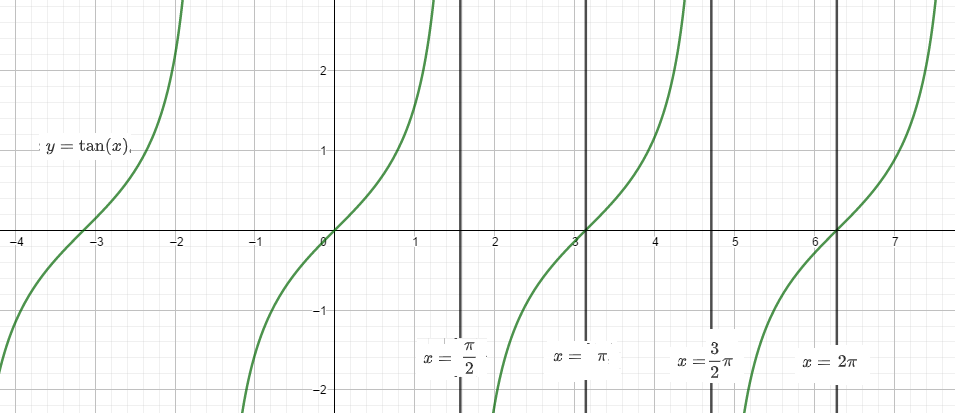
性质

• $\text{dom}f=\complement_\mathbb{R}\{(2k+1)\pi|k\in\mathbb{Z}\},\text{ran}f=\mathbb{R}$
• 对称性：f关于$(2k\pi,0)$中心对称（$k\in\mathbb{Z}$）。
• 奇偶性：奇函数。
• 周期性：最小正周期为$2\pi$
• 连续性：在$(2k+1)\pi$处不连续（$k\in\mathbb{Z}$）。
• 可导性：在$(2k+1)\pi$处不可导（$k\in\mathbb{Z}$）。
• 单调性：在区间$[2k\pi-\pi,2k\pi+\pi]$上单增（$k\in\mathbb{Z}$）。
• 凹凸性：在区间$[2k\pi,2k\pi+\pi]$上为凹函数，在区间$[2k\pi-\pi,2k\pi]$上为凸函数。

$f:y=A\sin(\omega x+\varphi)$

设$k\in\mathbb{Z}$。

求特殊点、特殊区间的核心思想：

考虑令$t=\omega x+\varphi$，则化为了乘了一个常数的普通的“正弦函数”。求其特殊点（或特殊区间），再将$t=\omega x+\varphi$代入，解方程（或不等式组）。

• 最小正周期：$|\dfrac{2\pi}\omega|$

• 最值

$y_{\max}=A,\omega x+\varphi=2k\pi+\dfrac\pi2$

$y_{\min}=-A,\omega x+\varphi=2k\pi-\dfrac\pi2$

由此解出。

• 对称性：

对称中心：解$\omega x+\varphi=k\pi$。对称中心为$(x,f(x))$。

对称轴：解$\omega x+\varphi=k\pi+\dfrac\pi2$。

• 单调区间：

增区间：$2k\pi-\dfrac\pi2\le\omega x+\varphi\le2k\pi+\dfrac\pi2$

减区间：$2k\pi+\dfrac\pi2\le\omega x+\varphi\le2k\pi+\dfrac32\pi$

• 凹凸区间：留作读者思考。

例题

例题1

以下命题正确的是（）
A.周期函数一定有最小正周期。
B.$y=\sin|x|$为最小正周期为$\pi$的偶函数。
C.$y=|\sin(x)|$为最小正周期为$2\pi$的偶函数。
D.$y=\sin(x+\dfrac\pi2)$的图像关于y轴对称。

解析

本题考查了基本的概念。
对于A，常数函数无最小正周期。
对于B，该函数并非周期函数。
对于C，最小正周期为$\pi$。
对于D，由平移关系，$y=\sin(x+\dfrac\pi2)$即$\cos(x)$。故D正确。

例题2

(1)求$y=\cos^2(x)+sin(x)+1$值域
(2)求$y=\dfrac{2\sin(x)+1}{\sin(x)-2}$值域

解析

(1)采用换元法。令$t=\sin(x)$，有$y=1-t^2+t+1=-t^2+t+2(-1\le t\le1)$，由二次函数的知识容易得到。
(2)采用换元法。令$t=\sin(x)$，有$y=\dfrac{2t+1}{t-2}(-1\le t\le1)$。同余容易求出答案。

关于换元

换元是一种非常重要、应用广泛的解题方法，在数学的各大领域都有强大的功效。
本题采用的方法即以元换式，将三角函数化归为我们熟知的二次函数和分式。
在看出式中有很多相同或相似的整体时，应当考虑以元换式。
对于本题的(1)，应当联想到利用三角函数的”平方关系“来把两项化为同名函数。之后，显然y便成为了关于$\sin(x)$的二次函数。这样问题也便迎刃而解。
这一思想将会在后面的章节被广泛运用。希望到那时，你会认为采用换元是显然的。
本题是一个非常简单的题目，因此不再赘述。

例题3

求$f(x)=1+\dfrac{2x+\sin(x)}{x^4+x^2}$的最大值与最小值之和。

错解

令$g(x)=\dfrac{2x+\sin(x)}{x^4+x^2}$，显然g为奇函数。故g的最大值与最小值关于原点对称。故$M+m=1+1=2$。

正解

例题3本是某道利用函数性质的典型题，但后来被笔者发现了问题，故挂在这里，提醒诸位注意函数的最大最小值的存在性。
在求最大最小值之前，首先要明确所求函数的有界性。
而本题的函数根本不存在最大值和最小值，其在竖直方向有渐近线$x=0$。
故正确的答案是：不存在。

三角函数线（几何定义）

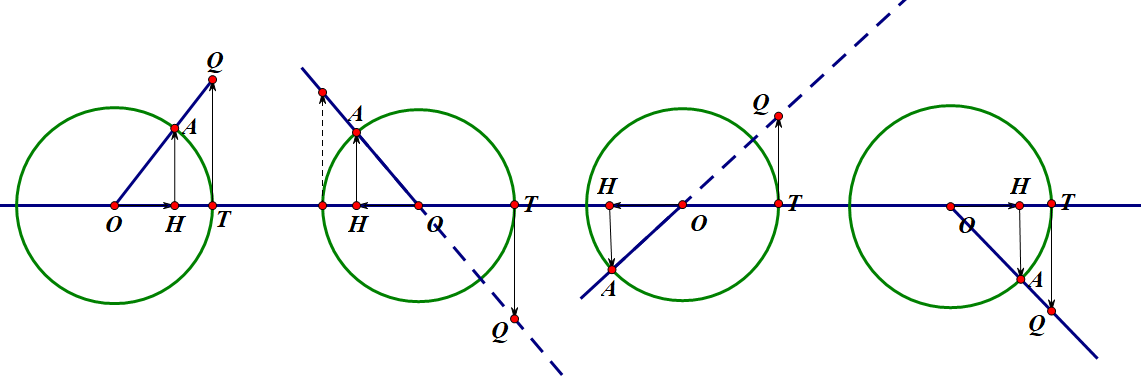
建立平面直角坐标系，设$\alpha$对应的射线$OA$，以原点为圆心作单位圆（半径为1的圆），则：

• $\vec{HA}=\sin(\alpha)$：正弦线
• $\vec{OH}=\cos(\alpha)$：余弦线
• $\vec{TQ}=\tan(\alpha)$：正切线

简单例题

比较大小：$\sin\dfrac{5\pi}7,\cos\dfrac{2\pi}7,\tan\dfrac{2\pi}7$

解析

作三角函数线易得。需要注意到$\dfrac{5\pi}7$与$\dfrac{2\pi}7$对应射线关于y轴对称。

常用公式

诱导公式

所谓诱导公式，即将$k\cdot\dfrac\pi2+x$的三角函数转化为$x$的三角函数。

只需掌握三角函数的图象。因为诱导公式的本质即平移。

和差角公式

$\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)$
$\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$
$\tan(x+y)=\dfrac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)}$

以上合角公式。差角公式按照奇偶性修改符号即可。

同角三角函数关系式

• 倒数关系：$\sin(x)\csc(x)=1,\cos(x)\sec(x)=1,\tan(x)\cot(x)=1$
• 商数关系：$\tan(x)=\dfrac{\sin(x)}{\cos(x)},\cot(x)=\dfrac{\cos(x)}{\sin(x)}$
• 平方关系：$\sin^2(x)+\cos^2(x)=1,1+\tan^2(x)=\sec^2(x),1+\cot^2(x)=\csc^2(x)$

证明十分容易，此处略去。

可以用如下图示：

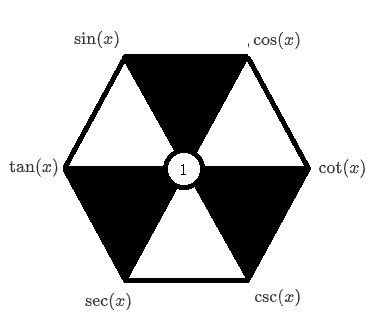
其中三角形上两个顶点的平方和即下顶点平方，六边形对角线两顶点相乘为1。

有一个高考内常考的内容：需要化简分式三角函数（分子或分母含有三角函数）时：

• 可以考虑利用分式基本性质，分子分母同时乘或除以一个三角函数，达到化简目的。
• 如果乘以或除以一个三角函数时，有常数项无法除尽，可以考虑利用“平方和（差）为1的关系”，将常数项化为三角函数的平方和（差）。

一个简单的例题

已知$\tan(x)=2$，求：$\dfrac1{\sin^2(x)-\sin(x)\cos(x)-\cos^2(x)}$

解析

分子化为$\sin^2(x)+\cos^2(x)$后，分子分母同时除以$\cos^2(x)$。

其余题目同理。

倍角公式

• $\sin(3x)=4\sin(x)\sin(60°-\alpha)\sin(60°+\alpha)$
• $\cos(3x)=4\cos(x)\cos(60°-\alpha)\cos(60°+\alpha)$
• $\tan(3x)=\tan(x)\tan(60°-\alpha)\tan(60°+\alpha)$
• $\sin(3x)=3\sin(x)-4\sin^3(x)$

例题

求$\sin1°\sin2°\sin3°\cdot\cdot\cdot\sin89°$

解析

可以考虑分组。将其分为：$1,59,61;2,58,62;\cdot\cdot\cdot;29,31,89$。
则原式=$(\dfrac14)^{29}\sin3°\sin6°\cdot\cdot\cdot\sin87°\sin30°\sin60°$
再继续分组即可。注意最后需要计算$\sin36°$的值。这个值有些复杂，因此只需要记忆有$\cos36°=\dfrac{1+\sqrt5}4$，再考虑确定正弦值的符号，利用“平方关系”得出$\sin36°$。
最终答案为$\sqrt{\dfrac{180}{2^{179}}}$。

注意，还可以利用复数章节的一个结论。

$\sin\dfrac\pi n\sin\dfrac{2\pi}n\cdot\cdot\cdot\sin\dfrac{(n-1)\pi}n=\dfrac{n}{2^{n-1}}$。

和差化积、积化和差公式

• $\sin(x)+\sin(y)=2\sin\dfrac{x+y}2\cos\dfrac{x-y}2$
• $\sin(x)-\sin(y)=2\cos\dfrac{x+y}2\sin\dfrac{x-y}2$
• $\cos(x)+\cos(y)=2\cos\dfrac{x+y}2\cos\dfrac{x-y}2$
• $\cos(x)-\cos(y)=-2\sin\dfrac{x+y}2\sin\dfrac{x-y}2$
• $\cos(x)\cos(y)=\dfrac12(\cos(x-y)+\cos(x+y))$
• $\sin(x)\sin(y)=\dfrac12(\cos(x-y)-\cos(x+y))$
• $\sin(x)\cos(y)=\dfrac12(\sin(x+y)+\sin(x-y))$
• $\cos(x)\sin(y)=\dfrac12(\sin(x+y)-\sin(x-y))$

以上8式，即和差化积、积化和差公式。

例题1

已知$\sin(x)+\sin(y)=\dfrac12,\cos(x)+\cos(y)=\dfrac13$，求$\cos(x-y),\sin(x+y),\tan(x+y)$。

解析

利用完全平方公式：
$\sin^2(x)+\sin^2(y)+2\sin(x)\cos(y)=\dfrac14\tag{*}$
$\cos^2(x)+\cos^2(y)+2\cos(x)\cos(y)=\dfrac19\tag{**}$
相加：$2+2\sin(x)\sin(y)+2\cos(x)\cos(y)=\dfrac14+\dfrac19\tag*{.}$
$2\cos(x-y)=\dfrac{13}{36}-2,\cos(x-y)=-\dfrac{59}{72}\tag{1}$。
题目条件的两式相乘：
$\dfrac16=\sin(x)\cos(x)+\sin(y)\cos(y)+\sin(x)\cos(y)+\cos(x)\sin(y)\tag*{.}$
$=\dfrac12(\sin(2x)+\sin(2y))+\sin(x+y)\tag*{.}$
$=\dfrac12\cdot2\sin(x+y)\sin(x-y)+\sin(x+y)\tag*{.}$
$\dfrac16=\sin(x+y)(-\dfrac{59}{72})+\sin(x+y)\tag*{.}$
故
$\sin(x+y)=\dfrac{12}{13}\tag{2}$
利用$(*)$和$(**)$，可以得到：
$\dfrac19-\dfrac14=\cos(2x)+\cos(2y)+2\cos(x)\cos(y)-2\sin(x)\sin(y)\tag*{.}$
$=2\cos(x+y)\cos(x-y)+2\cos(x+y)\tag*{.}$
$2\cos(x+y)(-\dfrac{59}{72})+2\cos(x+y)\tag*{.}$
故
$\cos(x+y)=-\dfrac5{13}\tag*{.}$
$\tan(x+y)=-\dfrac{12}5\tag{3}$

如何想到本题的处理方式？

(1)我们注意到，$\cos(x-y)$应当表示为“同名积和”，即x和y的sin值乘积与cos值乘积之和。那么就要考虑构造这一“纯项积和”。考察题目条件，可以理解为：题目给定了$u+v$，我们要求$uv$。不难联想到完全平方公式。而考虑到两式相加后多余的平方项会成为常数项，问题便迎刃而解。
(2)对于$\sin(x+y)$的处理，应当表示为“异名积和”，即$\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)$。依然用类似(1)的思想：题目中给出了$u+v,p+q$，我们要求$uq+vp$，显然可以考虑将$u+v$与$p+q$相乘。此时再利用2倍角公式、和差化积公式来处理剩下的部分，余下的推理就十分自然了。
(3)对于$\tan(x+y)$，可能有人会想到利用商数关系和平方关系，试图求出$\cos(x+y)$来求出$\tan(x+y)$。但这样做无法确定$\cos(x+y)$的符号。
考虑到$\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$，这是“同名积差”，处理方法和(1)几乎是相同的，显然应当利用$(*)(**)$相减来构造。

等差数列的正（余）弦值求和

引入

试求$\sum\limits_{j=1}^{n}\cos(a+jd)$。

解析

令原式=$F$，则：
$\sin\dfrac d2F=\sum\limits_{j=1}^{n}\sin\dfrac d2\cos(a+jd)=\sum\limits_{j=1}^{n}\sin\dfrac d2\cos\dfrac{a+jd+\dfrac d2+a+jd-\dfrac d2}2\tag*{.}$
$=\dfrac12\sum\limits_{j=1}^{n}(\sin(a+jd+\dfrac d2)-\sin(a+jd-\dfrac d2))\tag*{.}$
$=\dfrac12(\sin(a+nd+\dfrac d2)-\sin(a+\dfrac d2))\tag*{.}$
除以$\sin\dfrac d2$即可得到答案。

关于裂项

裂项的本质，即给定某数列的差分数列，求差分前的原数列。
我们会在数列中的“离散微积分”一节提到更加详细的内容。
对于本题的和式，如果十分熟悉“积化和差公式”，考虑到“积化和差公式”的第四式，只要构造出$x,y$，即可达到裂项目的；而由于等差数列的良好性质，这一$x,y$是十分容易构造，且仅可以构造出唯一一组的。

等差数列的正（余）弦值的$2^n$次方求和

• 思路：需要考虑$\cos^2(x)=\dfrac{1+\cos(2x)}2$，依次降次，再展开，继续降次。由于x构成等差数列，2x也构成等差数列，最后降到一次时即可利用“等差数列的正（余）弦值求和”来处理。

例题

求$\cos^4\dfrac\pi{16}+\cos^4\dfrac{3\pi}{16}+\cdot\cdot\cdot+\cos^4\dfrac{15\pi}{16}$。

解析

$\text{LHS}=(\dfrac{1+\cos\pi8}2)^2+\cdot\cdot\cdot\tag*{.}$
$=(\dfrac14+\dfrac12\cos\pi8+\dfrac14\cos^2\pi8)+\cdot\cdot\cdot+(\dfrac14+\dfrac12\cos{15\pi}8+\dfrac14\cos^2{15\pi}8)\tag*{.}$
$=\dfrac14+\cdot\cdot\cdot+\dfrac14+\dfrac12\cos\pi8+\cdot\cdot\cdot+\dfrac12\cos{15\pi}8+\dfrac14\cos^2\pi8+\cdot\cdot\cdot+\dfrac14\cos^2{15\pi}8\tag*{}$
$=2+0+\dfrac14(\dfrac{1+\cos\dfrac\pi4}2+\cdot\cdot\cdot+\dfrac{1+\cos\dfrac\pi4}2)=2+0+\dfrac14\times\dfrac12\times8=3\tag*{}$

事实上，可以求等差数列正（余）弦值k次方的和，这需要使用牛顿公式进行递推，这是多项式中的内容，故暂时略去。

万能公式

• $\sin(2x)=\dfrac{2\tan(x)}{1+\tan^2(x)}$
• $\cos(2x)=\dfrac{1-\tan^2(x)}{1+\tan^2(x)}$
• $\tan(2x)=\dfrac{2\tan(x)}{1-\tan^2(x)}$

以上3式，即万能公式。

万能公式主要用于换元，在做积分时就常常需要使用它。

Euler公式

您可能已经注意到，前面的恒等式都没有给出证明。这是因为这些内容在 Euler 公式的角度下是显然的。

$$e^{ix}=\cos(x)+i\sin(x)\tag{Euler}$$

由此公式可得：

$$\sin(x)=\dfrac{e^{ix}-e^{-ix}}{2i},\cos(x)=\dfrac{e^{i\pi}+e^{-i\pi}}2$$

其余三角函数同理。

证明 & 更加详细的内容请参考复数章节。

评论